logistic_saturation#

pymc_marketing.mmm.transformers.logistic_saturation(x, lam=0.5)[source]#

Logistic saturation transformation.

\[f(x) = \frac{1 - e^{-\lambda x}}{1 + e^{-\lambda x}}\]

The logistic saturation function reaches the half-saturation point at \(x = \frac{ln(3)}{\lambda}\). This means the half-saturation point is approximately \(1/\lambda\). If you want to set a prior on the exact half-saturation point, you can use the inverse_scaled_logistic_saturation function, available in this package.

(Source code, png, hires.png, pdf)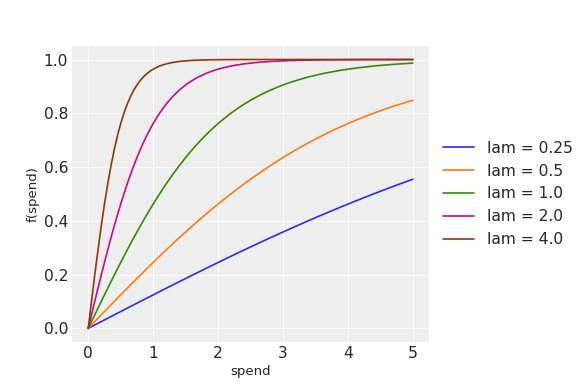

../../_images/pymc_marketing-mmm-transformers-logistic_saturation-1.png

Parameters:

xtensor: Input tensor.
lamfloat or array_like, optional, by default 0.5: Represents the efficiency of the channel. Larger values represent a more efficient channel.

Returns:

tensor: Transformed tensor.